Project summary
Project title
The discrete minimum-weight design of modular building systems subjected to multiple performance constraints using an optimality criteria method
Project lead
Dr Zixiao Wang
In recent years, rapid urbanisation trends have created pressing demands for affordable residential and office space in many major cities of developed and developing countries.
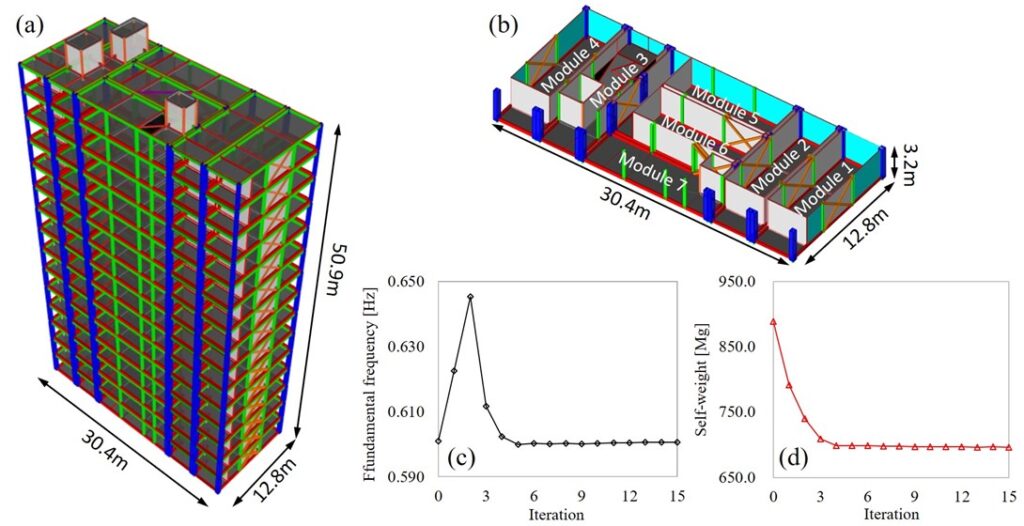
In this background, steel modular building systems (MBS), underpinned by modern methods of construction and design for manufacture/assembly (DfMA) techniques, have gained massive momentum owing to their advantages such as safer manufacturing, better quality control, reduced waste generation, demountability/reusability, and faster construction speed [1 - 6]. In volumetric modular construction illustrated in Fig. 1 (a), three-dimensional, factory-made building modules are assembled on-site to form a complete building through inter-module and module-to-foundation connections, as shown in Fig. 1(b). By adopting this construction method and DfMA considerations, more than three-fourths of the construction process can be completed off-site [7], with potential steel savings up to 26% to 31% [8]. As an increasingly viable proposition for the ongoing housing crisis, an important aspect of MBS that must be considered in design is their material usage and sustainability compared to other conventional building structural systems. Indeed, in 2015, the manufacturing of materials for building construction was estimated to account for 11% of global energy-related CO2 emissions [9]. One crucial strategy for reducing the building industry's embodied carbon footprint is to ensure material utilisation [10, 11].
In this setting, this research project aims to develop a minimum-weight design framework for MBS under multiple, commonly considered structural performance constraints using an optimality criteria (OC)-based sizing optimisation method adapted from the formulations in Venkayya [12].
In typical building design, these constraints can be either the lower limits on natural frequencies or critical buckling loads or upper limits on nodal displacements or member stresses under a given loading condition. The continuous-valued sizing optimisation process is achieved by an iterative, numerically stable algorithm (for modifying the members sizes towards the global optimum) and is largely expedited by an efficient, high-quality gradient estimation scheme together with parallel computing techniques.
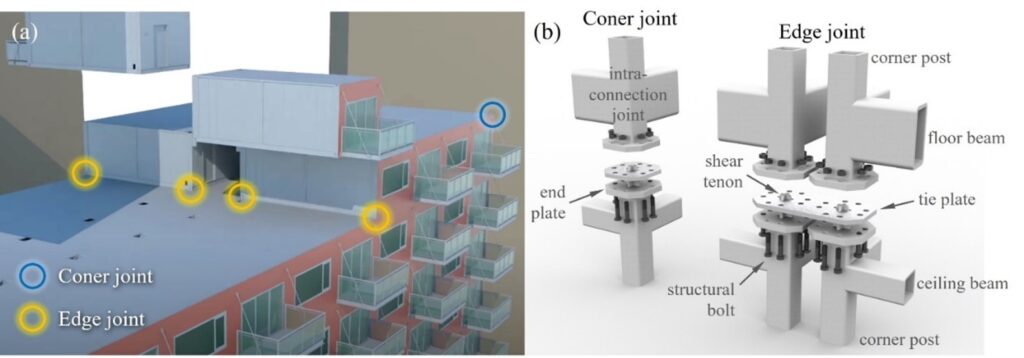
Fig. 1 (a) assembly of three-dimensional building modules with corner and edge inter-module joints (VectorBloc corp., (2016). VectorBloc Standardized Modular Construction System); and (b) assembly view of a possible design of bolted corner and edge joints.